动态规划
子问题图刻画了子问题之间的依赖关系,图上的边数点数与运行时间成正比
钢条切割
更简单的求解方式
矩阵连乘
总括号化方案数
为卡特兰数,可能是指数级
最优子结构
证明方法 剪贴黏贴技术cut and paste
无权最长路径不符合 无权最短路径符合
因为无权最长路径中子问题之间相关,将原问题划分成两个子问题A和B,A中使用了的顶点不能在B中使用(简单路径的要求)
重叠子问题
刻画子问题空间 保持子问题空间尽量简单,在钢条切割问题中是子问题空间中的问题是长度为i的钢条的最优切割问题。
只在必要时扩展它,在矩阵连乘问题中,是起始点为i,终点为j的子问题
动态规划问题的时间复杂度
1.子问题总数和每个子问题的选择数 两者的乘积
2.子问题图
最长公共子序列问题
LCS的最优子结构

试图简单阐释一下证明思路 如懂
1.zk一定是延伸到了X和Y的末尾,否则Z可以更长,与Z是LCS矛盾
如何证明Zk-1也是LCS,如果存在更长的Xm-1和Yn-1的LCS W,那么Z可以更长
2和3 首先Z可以是Xm-1和Y的公共子序列…
什么是文件 vector<char>
什么是目录 map<string,file-ptr>
FAT
面对的情况 文件数少 块数也少 直接使用链表结构
FAT-16中的16代表”next数组”占用的bit
next数组标记了可能存在的该文件的下一块的位置或者坏块等等
文件是块的链表 但是链表的next数组被同一存放在一个位置利用了局部性,存储了多个备份保证安全
目录也是文件,目录的实际数据内容是目录项,其中也存放了文件的元信息
LL文法改造
消除左递归 提取公因子
如何消除间接左递归,保证产生式左右两端非终结符的单调性
ll star
支持二义,不支持间接左递归
三个大主题
优先级上升算法 将递归产生循环展开,附加上优先级,通过设置优先级实现左结合右结合和运算优先级。(左结合上升一级,右结合不变)
异常处理和从异常中恢复
following集合,一个动态分析的概念
(a*b)(c|d)
面对bc和bd,应该如何展开S呢?这似乎是一个LL(?) 的
lookahead dfa接受当前输入的整个前缀,告诉要选择哪个产生式
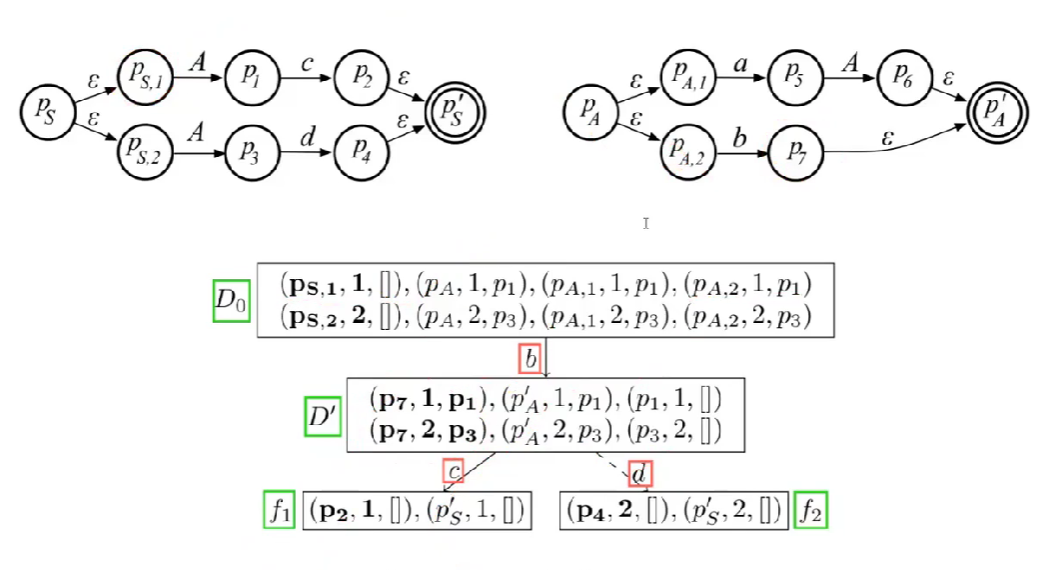
和NFA转DFA的算法类似,维护一个状态集合,(对于该文法)每个状态是一个三元组(当前状态,该状态选择的探索路径,递归调用栈(应当返回的状态))
也就是比NFA转DFA算法多了一个调用非终结符
Reorder Buffer/Renaming table
Renaming table维护寄存器名的映射
当新的指令被dispatch或者某条指令complete时应当分别被更新成 它在renaming table中的标签 和 实际值
乱序执行受限于指令的稳定提供-控制冒险
乱序发射dispatch本身不带来性能提升,因为还是受限于寄存器名称的相关
区分complete和commit
微体系
微体系是体系结构的实现
差分机
一个函数的值可以用做差分,最后用加法器填表计算
