动态规划

动态规划

拓扑序

背包问题

01背包

01背包

完全背包

完全背包

多重背包

多重背包

分组背包

分组背包

二维费用背包

集合：只从前i个物品中选，花费1不超过j，花费2不超过k的选法

状态计算：f[i][j][k] = max(f[i-1][j][k], f[i-1][j-v1[i]][k-v2[i]] + w[i][k])

三种不同划分的比较

以选法为例，最大值最小值同理

集合：恰好是k的选法

f[0]=1,f[k≠0]不存在，此处为0

集合：至少是k的选法

f[0]=1,f[k≠0]不存在，此处为0，且k为负数时合法，视为0

集合：不超过k的选法

f[k]=1

线性DP

数字三角形：从顶点出发到i,j的最大路径和

方格取数：所有从顶点出发走到(i1,k-i1)(i2,k-i2)的路径

按照两次路径的来自方向可分为四类

最长上升子序列

集合：所有以第i个数结尾的上升子序列

怪盗基德的滑翔翼：

所有上升子序列和下降子序列

最长公共子序列

集合：所有在第一个序列的前i个字母中，第二个序列的前j个字母中出现的子序列

按照第i，j个字母是否出现可分为四类

其中，i不出现j出现这一情况可用f[i-1,j]表示，虽然这个表示并不保证j一定出现，但不影响结果，i出现j不出现同理

i，j都不出现被包含于上述两种，i，j都出现时（即要求相等）时有f[i-1][j-1]+1

从而状态转移方程为：f[i][j] = max(f[i-1][j],f[i][j-1],f[i-1][j-1]+1)

最长公共上升子序列

集合：所有在第一个序列的前i个字母中，第二个序列的前j个字母中出现，且以b[j]结尾的公共上升子序列

按a[i]是否出现分为两类，a[i]不出现时即为f[i-1,j]

a[i]出现时(a[i]=b[j])，按照上一个元素为k=b[1...j-1]分为若干类，为f[i-1,k]+1

区间DP

石子合并

集合：将第i堆石子到第j堆石子合并成一堆石子的合并方式

f[i][j] = min(f[i,k]f[k+1,j]+s[i,j])

环形石子合并

可将题目看作在相邻的石子中连边，一共连n-1条边，根据“缺口”位置在石子合并的基础上再多一重循环 O(n^4)

要求的是n条长度为n的链上的最小值，可以发现将链重复两边，可以在这条长度为2n的链上找到所有上述的链

状态压缩DP

蒙特里安的梦想

只枚举横向摆放的情况

f[i,j]对应第i列，被上一列伸出状况以二进制数j表示

与f[i-1,k]应满足 j&k=0 j|k不存在连续奇数个零

f[0,0]=1

答案为f[m,0]

最短Hamilton路径

集合：所有从0走到j，经过的点为二进制表示i的路径

小国王

集合：只摆在前i行，摆了j个国王，第i行摆放状态是k的集合

转移：f[i][j][a]是所有满足a&b==0和a|b没有相邻的1的bf[i-1][j-count(a)][b]的和

玉米田

集合：只摆在前i行，第i行摆放状态是j的集合

转移：f[i][a]是所有满足a&b==0和a，b都没有相邻的1的bf[i-1][j-count(a)][b]的和

炮兵阵地

集合：只摆在前i行，第i-1行摆放状态是j，第i行摆放状态是k的集合

转移：f[i][a][b]是所有满足a,b,c在相同位上不同时有1且a,b相邻3位上至多只有一个1的f[i-1][c][a]+b中1的个数 的最大值

树形DP

没有上司的舞会

集合：所有以u为根的树中选择，选和不选u的方案

有依赖的背包问题

集合：所有以u为根的树中选择，体积不超过j的方案

树的最长路径

dfs从子节点更新到父节点，以该节点为根且从不同子节点出发的最长和次长的路径，是该节点向下的路径

树的中心

dfs从子节点更新到父节点，以该节点为根且从不同子节点出发的最长和次长的路径，是该节点向下的路径

再dfs从父节点更新到子节点，子节点的向上路径是父节点向上或向下（向下不能是该子节点）的最大路径加上子节点到父节点的路径

二叉苹果树

有依赖的背包问题

f[i][j]以i为根的树中选j条边的最大价值

战略游戏

类似没有上司的舞会

集合：以i为根的树中，点i选或不选的所有选法

f[i][0]=f[s1][1]+…

f[i][1]=1+min(f[s1][0],f[s1][1])+…

皇宫看守

集合：以i为根的树中，点i状态为j的所有选法

被父节点看到f[i][0]=Σmin(f[j][1],f[j][2])

被子节点看到 任选一个子节点为状态2，其余min(f[j][1],f[j][2]) 所有这样的最小值

自己f[i][2]=Σmin(f[j][0],f[j][1],f[j][2])+w[i]

数位DP

一般用前缀的方式计算，注意自己定义的是0-n中还是1-n中

计数问题

计算0-n中每个数字x在每个位上的出现次数（能构造出多少个数在某位上有x）

将n的数位分为三部分l mid r

先枚举l部分小于l的数

当计算0时，l部分须大于等于1，当计算非0时，l部分可以为0。然后r部分可以任取

再计算r部分时（即枚举l部分等于l的数）（l=0且x=0时不计算，不存在这种有前导0的数），若mid=x，则r部分可以取0-r，若mid>x，则r部分任取

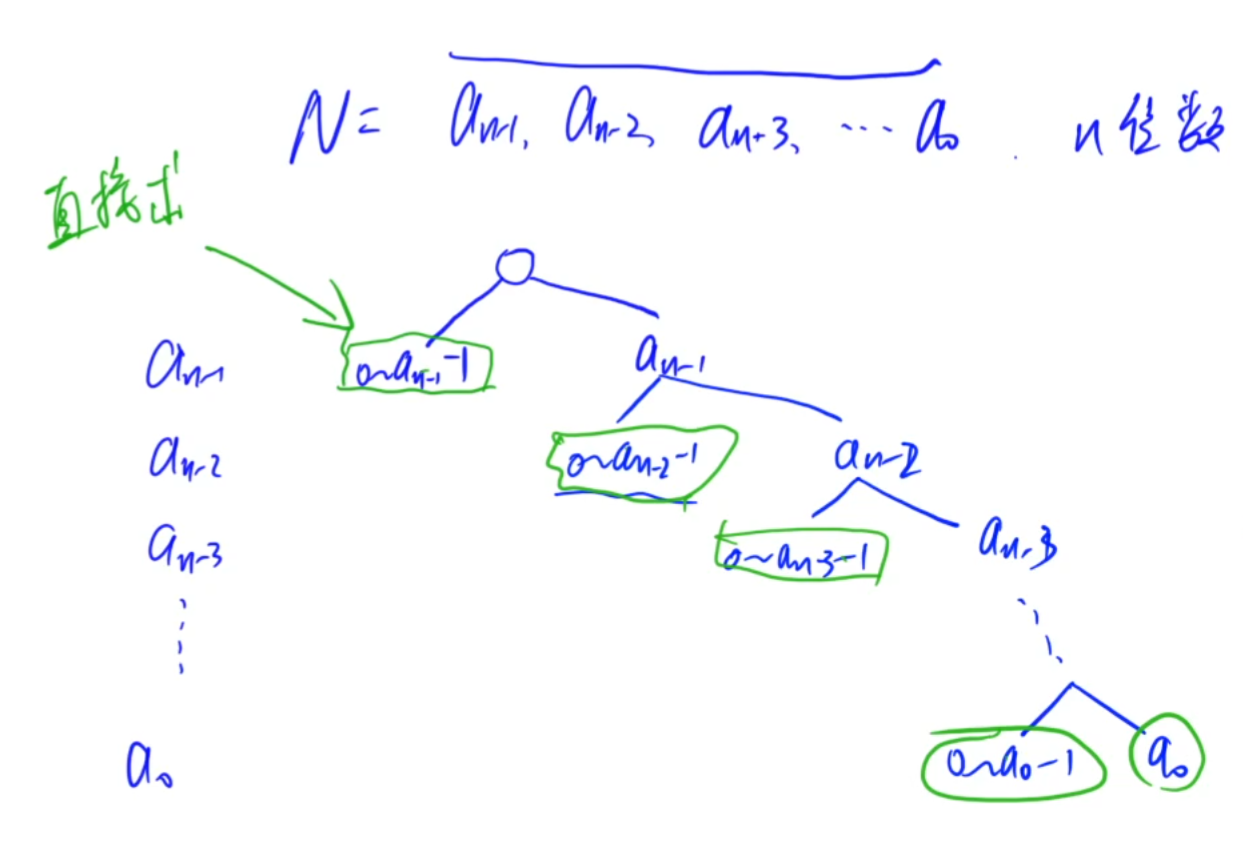
度的数量

即求0~n中有多少数是b进制表示下只含有k个1，其余皆为0的数

从高位往下看，若该位大于1，则可以取遍0到全是1的情况（可以直接计算出），直接break，若等于1，则有两种选择，一种该位置为0，在剩下的数中放1（可以直接计算出）。一种该位置为1，剩下的数中能放的1减少。最后记得处理1枚举完的情况

数字游戏

求不降数数量

取0-an-1-1时，用动态规划求出

取an-1时，保证比上一位不降

集合：最高位为j，且共有i位的不降数

f[i][j]=Σf[i-1][k](k>=j)

Windy数

注意(0)137不会被计算到f[4][0]，含前导零的情况要额外加一遍

或者说，设该数共n位，最高位取0的情况（1-99999999（n-1 个九））实际上是Σf[1~n-1][0~9]

恨七不成妻

T[i][j][a][b]i位数，最高位为j，该数模7余a，各位数字模7余b

T[i][j][a][b]由T[i-1][k][a-j*10^(i-1)][b-j]转移

$$\begin{array}{c}{S}_0^{\prime }+=S_0\\ v_1.s_0+=v_2.s_0\\ S_1^{\prime }+=\overline{k{A}_1}+\overline{k{A}_2}+...+\overline{k{A}_{s_0}}=S_0\ast k\ast 10^n+S_1\\ v_1.s_1+=v_2.s_0\ast k\ast 10^{i-1}+v_2.s_1\\ S_2^{\prime }+={\overline{k{A}_1}}^2+{\overline{k{A}_2}}^2+...+{\overline{k{A}_{s_0}}}^2=S_0\ast (k\ast 10^n{)}^2+2\ast k\ast 10^n\ast S_1+S_2\\ v_1.s_2+=v_2.s_0\ast (k\ast 10^{i-1}{)}^2+2\ast k\ast 10^{i-1}\ast v_2.s_1+v_2.s_2\end{array}$$

记忆化搜索

滑雪

集合：所有从(i,j)开始滑的路径

状态机模型

集合：所有从前i个物品中选，状态为j的方案

大盗阿福

结点	可转移到
偷窃	不偷窃
不偷窃	不偷窃，偷窃

股票买卖IV

f[i][j][0]：第i天，已经进行完j次交易

f[i][j][1]：第i天，正在进行第j次交易

状态转移方程是：

f[i][j][0] = max(f[i-1][j][0], f[i-1][j][1]+w[i])

f[i][j][1] =max(f[i-1][j][1], f[i-1][j-1][0]-w[i])

结点	可转移到
持有	不持有，持有
不持有	不持有，持有

股票买卖V

结点	可转移到
持有	不持有的第一天，持有
不持有的第一天	不持有的第二天及之后
不持有的第二天及之后	不持有的第二天及之后，持有

f[i][0]=max(f[i-1][0],f[i-1][2]-w)

f[i][1]=f[i-1][0]+w

f[i][2]=max(f[i-1][1],f[i-1][2])

设计密码

集合：密码串的前i个字母的最后j个字母和模板串前j个字母匹配的方案

转移：f[i+1][u]=f[i][j1]+f[i][j2]+…

密码串的第i+1个字母选择a~z导致j转移到不同的u

f[0][0]=1 答案为f[n][0]+…+f[n][m-1]

单调队列优化

最大子序和

将问题分类为以序列中哪个元素为结尾的序列

引入前缀和后问题即为求s[k]-s[k-j] (1<=j<=m)的最大值，滑动窗口解决

旅行问题

环拉成链

记录每两个相邻点的油量与距离之差，则题意为所有前区间和大于等于0，也即所有长度为环的长度的窗口中区间和最小值大于等于0

顺时针下ii+n-1中最小为j，需满足s[j]-s[i-1]>=0，逆时针下i-n+1i，需满足s[j]-s[i+1]>=0

烽火传递

集合：1-i合法，且点燃第i个烽火台的方案

f[i]=min(f[j])+w[i] i-m<=j<i

绿色通道

二分，寻找满足时间不超过t的最长空题段 的最小值

最长空题段是上一题中的每多少个烽火台至少有一个烽火台的限制，时间是代价

f[i]=min(f[j])+w[i] i-limit-1<=j<i

修剪草坪

集合：从前i头牛中选的方案

由于不能连续选k个，根据在哪个牛不选来分类

f[i]=max(f[i-1],f[i-x-1]+s[i]-s[i-x]) 1<=x<=k i-k<=i-x<i

代表不选i-x牛，选i-x到i中的牛

单调队列计算使f[i-x-1]-s[i-x]最大的i-x

考虑x=i时，代表前i头中全选，应视f[i-x-1]为0

理想的正方形

对每行求滑动窗口，再对每列求

斜率优化

任务安排1，2

将启动时间对所有后续任务影响特殊处理

集合：前i个任务的方案

f[i]=min(f[j]+sumt[i]* (sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]))j<i

斜率优化

f[j]=(sumt[i]+s)*sumc[j]+f[i]-sumt[i] *sumc[i]-s *sumc[n]

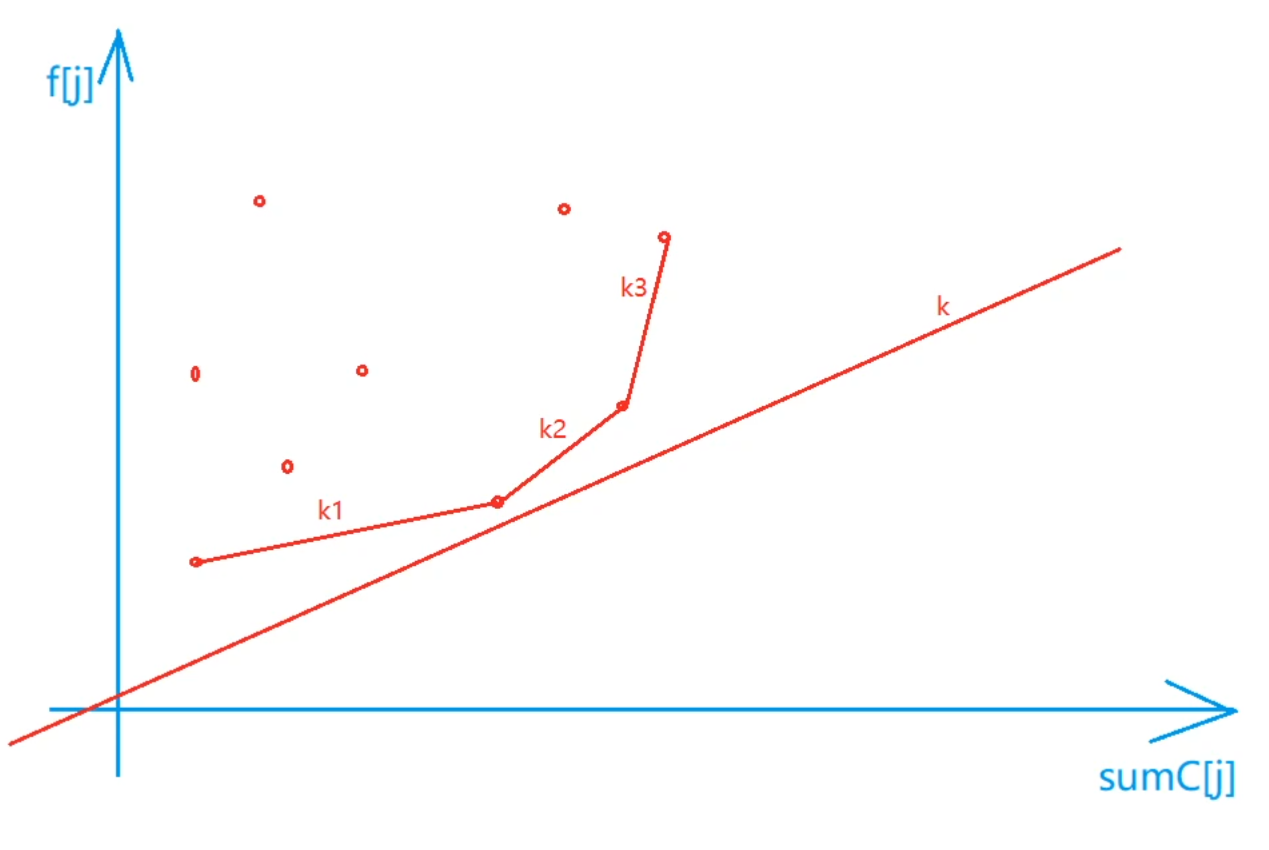
对于任意给定的i，视f[j]为y，sumc[j]为x，则斜率与j无关为定值且为非正无穷正数，取不同的x确定不同的f[i]

通过图像观察可知，只保留“凸包”上的点，找到第一个斜率大于k的点

在本题中，随着i递增，x递增，在插入的时候可以删除队尾不在凸包上的点，（待查询的）k也递增，因此查询的时候可以删除队头小于查询值的点

任务安排3

本题中斜率不是单调递增，只能二分查找

运输小猫

接到猫的最早时间是t[i]-d[i]，记作a[i]

人为将猫最早时间排序 接走i~j猫的最早时间为a[j]，等待时间为(j-i+1)*a[j]-s[j]+s[i-1]

f[j][i] j个饲养员，取前i只小猫的最小花费

f[j][i]=min(f[j-1][k]+a[i]*(i-k)-s[i]+s[k])

f[j-1][k]+s[k]=a[i]* k+f[j][i]-a[i]*i+s[i]

对任意给定i，视f[j-1][k]+s[k]为y，k为x，a[i]递增